
We're going to do some more work on it, but don't want to lose what we've done so far. Having done that, save it again as Projectile2. NOW SAVE THIS SPREADSHEET AS PROJECTILE1. Call the graph Projectile: Zero Air Resistance, label the axes " distance along ground" and " height above ground". Highlight cells D15 through E214, and click Chartwizard. Now, select cells A16 through E16 and copy all five columns down through E214. (Also, Bold and Right Justify A7, A8, A9, A10.) Then select these cells, click Bold, and Center justify. Put the appropriate names in B8, B9 and B10, and then enter some reasonable values, say, 10, 20, 30, 0.05, ready for when we construct the table. Click on B7, click Insert/Name/Define, it will suggest name g, click OK. In A7, A8, A9 and A10 write respectively g=, v_x_init=, v_y_init= and delta_t=.

(Of course, v_x isn't going to change, but we're going to need that column when we include air resistance, so we might as well put it in now.) Since we're interested in both velocity and position of the projectile as functions of time, we'll construct a spreadsheet with five columns: time, v_x, v_y, x, y. Of course, we also need to specify the time interval used in our discretization of the motion, we'll call it delta_t as usual. In contrast to our earlier spreadsheets on falling objects, we will now take the upward direction to be positive. There are three variables: the initial horizontal velocity, call it v_x_init, the initial vertical velocity v_y_init, and the acceleration due to gravity g.

Let's call it Projectile1, and write in A1 " Motion of a Projectile Under Gravity"
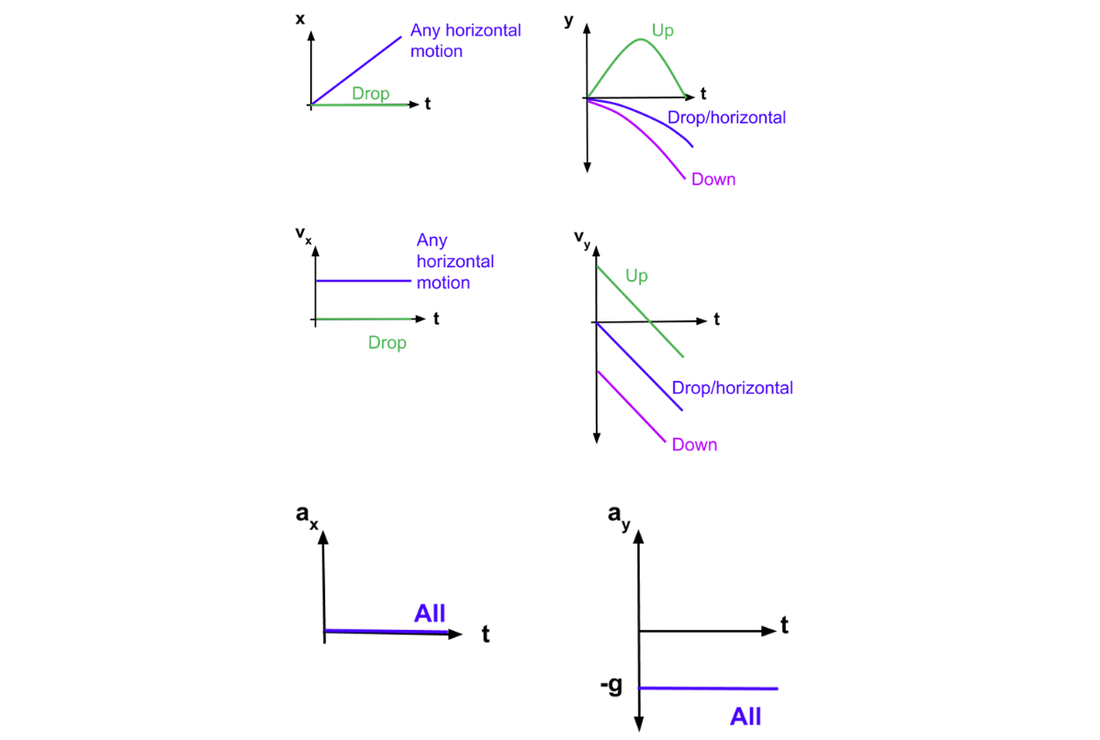
It's easy to reproduce this compound motion with a spreadsheet. Galileo argues that, if air resistance could be neglected, the horizontal motion was one at constant velocity, the vertical motion was one of uniform downward acceleration, identical to that of an object falling straight down. The first successful attempt to describe projectile motion quantitatively followed from Galileo's insight that the horizontal and vertical motions should be considered separately, then the projectile motion could be described by putting these together. HOME Using Spreadsheets for Projectile Motion


 0 kommentar(er)
0 kommentar(er)
